Il periodo di maggior rilevanza tecnico-scientifica è l’età ellenistica, periodo che va dal 323 a.C. (morte di Alessandro Magno) al 31 a.C. (battaglia di Azio, che segna la trasformazione dell’Egitto in provincia romana).
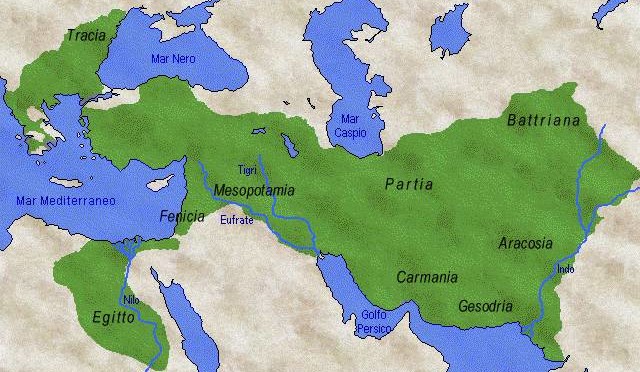
Alessandro iii, nato a Pella (Macedonia) nel 356 a.C., morto a Babilonia nel 323 a.C., fu imperatore del Regno di Macedonia dal 336 a.C. alla morte. Passò alla storia come “Magno” (dal latino magnus, grande) poiché in soli dodici anni estese il dominio macedone fino alla Valle dell’Indo, inglobando l’Impero persiano, l’Egitto, il Pakistan e l’Afghanistan.
L’ellenismo apportò notevoli sviluppi nel campo scientifico (anche se l’uso del termine “scientifico” è più propriamente utilizzabile solamente dalla fine del xvi secolo con l’introduzione del metodo scientifico da parte di Galileo Galilei); tuttavia questi sviluppi restarono allo stadio della teoria e, solo in pochi casi, furono tradotti in pratica. Anche in questi casi, spesso la finalità era puramente dimostrativa o scenica.
Come suggerisce Alexandre Koyré nel suo saggio Dal mondo del pressappoco all’universo della precisione (Torino : Einaudi, 2000), e nel saggio complementare di Pierre-Maxime Schuhl Perché l’antichità classica non ha conosciuto il macchinismo, esistono alcune ragioni principali per la mancata diffusione delle macchine nella Grecia antica. L’abbondanza di mano d’opera servile a basso costo portò a un disinteresse nella ricerca di applicazioni tecniche a supporto delle attività umane; tale situazione si stratificò socialmente in un pregiudizio riguardo la tecnica e il tecnico: il tecnico era colui che sovvertiva l’ordine naturale, manifestazione terrena della divinità.
Tale attitudine al dominio della tecnica si ritrova ancora oggi in termini quali “macchinazione”: esso ha il significato di “complotto”, “inganno” ai danni di qualcuno, ed è da far risalire anche all’uso delle macchine a fini teatrali, ove la funzione di queste era, in ultima analisi, di “ingannare” gli spettatori, di far loro credere qualcosa che in realtà non esiste.
“I Greci non ambivano a mutilare quell’opera d’arte che è il mondo, mutandone il volto. E c’è in questo una convinzione giusta e bella. Da Bacone in poi, il mondo è diventato per noi un magazzino, una miniera, un fondo al quale attingiamo senza prudenza”; ecco come Koyré riassume le posizione dei Greci rispetto alla tecnica (pp. 128-9 di Dal mondo del pressappoco all’universo della precisione).
Polo principale dello sviluppo teorico dell’epoca ellenistica è Alessandria d’Egitto, grazie alla presenza della dinastia greco-egizia dei Tolomei, fiorita tra il 305 e il 30 a.C., periodo grossomodo corrispondente alla durata dell’Ellenismo stesso. Il merito culturale della dinastia (in particolare di Tolomeo ii Filadelfo) fu quella di aver impiantato ad Alessandria il primo Museo (non nell’accezione moderna del termine, ma inteso come “luogo delle muse”, una sorta centro di ricerca) con adiacente una biblioteca. L’interesse dei Tolomei per la cultura si tradusse in mecenatismo, con invito ed accoglienza delle maggiori personalità letterarie e scientifiche del tempo.
 La figura alla quale si deve la più potente teorizzazione (in ambito geometrico-matematico) fu Euclide (Alessandria d’Egitto 325-265 a.C.) padre della geometria che da lui prese il nome e noto come autore degli Elementi, maggiore opera sulla geometria dell’antichità. Il suo merito in realtà sta nell’aver codificato per primo le proposizioni logiche relative alla geometria, dividendole in:
La figura alla quale si deve la più potente teorizzazione (in ambito geometrico-matematico) fu Euclide (Alessandria d’Egitto 325-265 a.C.) padre della geometria che da lui prese il nome e noto come autore degli Elementi, maggiore opera sulla geometria dell’antichità. Il suo merito in realtà sta nell’aver codificato per primo le proposizioni logiche relative alla geometria, dividendole in:
– assiomi (proposizioni logiche immediatamente ratificabili, definite vere dall’evidenza):
1. cose uguali ad una stessa cosa sono uguali tra loro;
2. aggiungendo (quantità) uguali a (quantità) uguali le somme sono uguali;
3. sottraendo (quantità) uguali da (quantità) uguali i resti sono uguali;
4. cose che coincidono con un’altra sono uguali all’altra;
5. l’intero è maggiore della parte;
– postulati (proposizioni il cui grado di evidenza è leggermente minore dell’assioma; si tratta di assunzioni che consentono di definire in modo più operativo le verità assiomatiche):
1. un segmento di linea retta può essere disegnato unendo due punti a caso;
2. un segmento di linea retta può essere esteso indefinitamente in una linea retta;
3. dato un segmento di linea retta, un cerchio può essere disegnato usando il segmento come raggio ed uno dei suoi estremi come centro;
4. tutti gli angoli retti sono congruenti tra loro;
5. se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, prolungando le due rette, esse si incontreranno dalla parte dove la somma dei due angoli è minore di due angoli retti.
Dal quinto postulato, in particolare, si deduce che “data una qualsiasi retta r ed un punto P non appartenente ad essa, è possibile tracciare per P una ed una sola retta parallela alla retta r data” (assioma di Playfair).